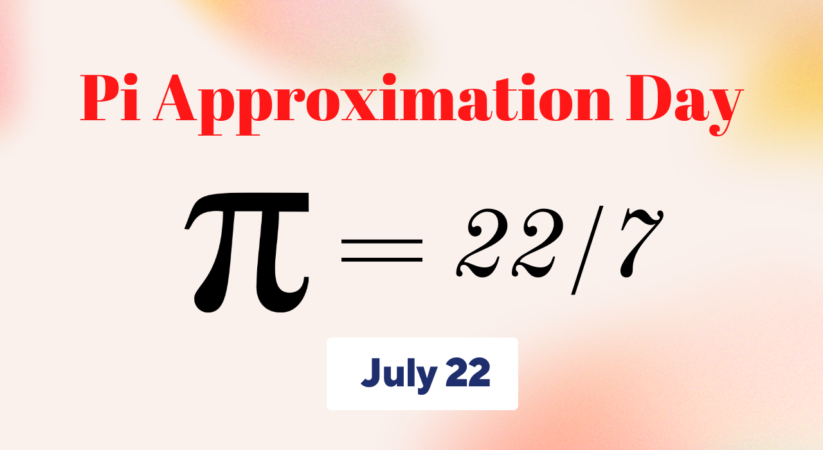Pi Approximation Day, also known to as Casual Pi Day, honours the number pi. Pi represents the proportion between a circle’s diameter and circumference. On July 22, a day specifically dedicated to the mathematical constant pi (π), Pi Approximation Day is observed.
What is Pi Approximation Day?
Pi Approximation Day is celebrated globally on July 22 each year. There is a special reason why this day is observed on July 22. The fraction 22/7 is an approximation of Pi. Since the fraction 22/7 represents the number pi, this day is observed annually on July 22. Here, the numerator 22 represents the date (the 22nd day of the month) and the numerator 7 represents the month in the fraction 22/7, which denotes Pi (July).
Surprising Facts About Pi:
Here are some interesting facts related to our beloved constant Pi:
– Since pi is not equal to the ratio of any two whole numbers, it is irrational. Since its numbers do not repeat, an approximation like 3.14 or 22/7 is frequently used in calculations.
– The value of pi to 39 decimal places is: 3.141592653589793238462643383279502884197.
– The Babylonians calculated the perimeter of a hexagon encircled by a circle and used 3,125 to approximate pi, supposing that the ratio of the hexagon’s perimeter to the circle’s circumference was 24/25.
– The Rhind papyrus suggests that the ancient Egyptians used a value of 256/81, or roughly 3.16045.
– Archimedes made a significant advancement by coming up with a strategy to calculate pi with any desired level of accuracy. He obtained the top and lower bounds by inscribing and circumscribing regular polygons around a circle, and the result was 223/71 22/7, or an average value of almost 3.1418.
– Archimedes also showed that the ratio of a circle’s area to its square of radius is a constant.
– By the end of the 17th century, new techniques for mathematical analysis in Europe gave rise to more accurate approaches to calculate infinite series-based pi. For instance, Sir Isaac Newton easily calculated 16 decimal places using his binomial theorem.
– Early in the 20th century, Indian mathematician Srinivasa Ramanujan created extremely effective methods for computing pi, which were later incorporated into computer algorithms.
– Early in the 21st century, computers calculated pi to 31,415,926,535,897 decimal places, as well as to its two quadrillionth digit when expressed in binary (0).
– Numerous mathematical problems involving the lengths of arcs or other surfaces, such as the areas of ellipses, sectors, and other curved surfaces, as well as the volumes of different solids, involve the number pi.
– Pi is employed in various physics and engineering formulas to describe periodic phenomena including pendulum motion, string vibrations, and alternating electric currents.
- Hong Kong will launch ETFs for Bitcoin and Ethereum on April 30 - April 25, 2024
- WhatsApp is now enabling passkey features for iPhone users - April 25, 2024
- Real Estate 2024: 7 Pennsylvania Cities Where Price Dropping in Housing Market - April 25, 2024